I love Math: Perpangkatan dan akar

Sudahkah hafal bilangan berpangkat??? taukah kalian tentang definisi bilangan berpangkat??
Yuuuk kita pelajari disini….
Bilangan berpangkat yang paling kita hafal adalah bilangan berpangkat dua dan berpangkat tiga, nah…untuk mempelajari materi-materi lanjutan, baik materi bilangan pangkat bulat positif, bilangan bulat negatif maupun bilangan berpangkat pecahan(akar), kita harus tau lebih dalam tentang definisi perpangkatan itu sendiri !

Let’s check this out …

Pangkat Bulat Positif

$a^n=\underset{sebanyak\;\; n}{a\times a\times a\times...\times a\times a}$

contoh :
1. $10^2=10\times 10=100$

2. $3^3=3\times 3\times3= 27$

3. $(-5)^4=(-5)\times (-5)\times (-5)\times (-5)= 625$

Pangkat Bulat Negatif

$\begin{align*}a^{-n} & = & \frac{1}{a^n}\\ & = & \underset{sebanyak\;\; n}{\frac 1a\times \frac 1a\times \frac 1a\times...\times \frac 1a} \end{align*}$

Contoh :
1. $2^{-5}=\frac{1}{2^5}=\frac 12\times \frac 12\times \frac 12\times \frac 12\times \frac 12=\frac{1}{32}$

2. $(-3)^{-3}=\frac{1}{(-3)^3}=\frac {1}{-3}\times \frac{1}{-3}\times \frac{1}{-3}=-\;\frac{1}{27}$

3. $\frac{1}{10000}=\frac{1}{10^4}=10^{-4}$

4. $7a^{-5}=7.\frac{1}{a^5}=\frac{7}{a^5}$

hmmmmm…..kalau sudah tahu prinsip perpangkatan, coba bikin tabel perpangkatan supaya mudah dalam menghafal,ok..???!!
Sekarang kita lihat aturan dalam perpangkatan yuuuuuuk…

Aturan Pangkat

$a^0=1$

$a^n.a^m=a^{n+m}$

$\frac{a^n}{a^m}=a^{n-m}$

$(a^n)^m=a^{n.m}$

$(a.b)^n=a^n.b^n$

$\left ( \frac ab \right )^n=\frac{a^n}{b^n}$

Mari kita lihat contoh berikut ini….
1. $2^3.2^2=2^5=32$

2. $\frac{5^6}{5^{10}}=5^{-4}=\frac{1}{625}$

3. $(2^2)^3=2^6=64$

4. $(-2a)^3=(-2)^3.a^3=-8a^3$

5. $\left (\frac 5q \right )^3=\frac{5^3}{q^3}=\frac{125}{q^3}$

Contoh soal-soal dan pembahasan aturan pangkat mari kita simak yang berikut ini :
Nyatakan dalam bentuk pangkat positif yang paling sederhana !!!!!

$\begin{align*}1.\;\;(-5a^{-2}b^3)^2&=&(-5)^2(a^{-2})^2(b^3)^2\\&=&25a^{-4}b^6\\&=&\frac{25b^6}{a^4}\end{align*}$

$\begin{align*}2.\;\left (\frac{2}{a^3} \right )^{-4} & = & \frac{1}{\left (\frac{2}{a^3} \right )^{4}}\\ & = & \left ( \frac{a^3}{2} \right )^4\\ & = & \frac{a^{12}}{2^4}\\ & = & \frac{a^{12}]}{16}\end{align*}$

$\begin{align*}3.\;\;\frac{3p^2q^{-5}}{ab^4}\times \frac{a^3b^{-2}}{12p^{-3}q^7}&=&\frac{3{\color{Red} a^3}{\color{DarkBlue} b^{-2}}{\color{DarkGreen} p^2}{\color{Purple} q^{-5}}}{12{\color{Red} a}{\color{DarkBlue} b^4}{\color{DarkGreen} p^{-3}}{\color{Purple} q^7}}\\&=&\frac 14.{\color{Red} a}^{3-1}.{\color{DarkBlue} b}^{-2-4}.{\color{DarkGreen} p}^{2-(-3)}.{\color{Purple} q}^{-5-7}\\&=&\frac 14.a^2.b^{-6}.p^5.q^{-12}\\&=&\frac{a^2p^5}{4b^6q^{12}}\end{align*}$

Bilangan akar dinotasikan dengan

$\sqrt[n]{a}$ dibaca ” akar pangkat n dari a ” dimana n adalah indeks dan a adalah radikan .

Contoh :
1. $\sqrt{3}$ dibaca akar pangkat 2 dari 3 dengan indeks 2 dan radikan 3

2. $\sqrt[3]{2}$ dibaca akar pangkat 3 dari 2 dengan indeks 3 dan radikan 2

Operasi Bentuk Akar Pangkat 2

$p{\color{Red} \sqrt{a}}+q{\color{Red} \sqrt{a}}=(p+q){\color{Red} \sqrt{a}}$

$p{\color{Red} \sqrt{a}}-q{\color{Red} \sqrt{a}}=(p-q){\color{Red} \sqrt{a}}$

$\sqrt{{\color{Red} a}}\times \sqrt{{\color{Red} b}}=\sqrt{{\color{Red} ab}}$

$\frac{\sqrt{{\color{Red} a}}}{\sqrt{{\color{Red} b}}}=\sqrt{{\color{Red} \frac ab}}$

Contoh :
1. ${\color{Red} 2}\sqrt{5}+{\color{Red} 3}\sqrt{5}-\sqrt{5}=({\color{Red} 2}+{\color{Red} 3}-{\color{Red} 1})\sqrt{5}={\color{Red} 4}\sqrt{5}$

2. ${\color{Red} 4}\sqrt{{\color{DarkGreen} 2}}\times {\color{Red} 3}\sqrt{{\color{DarkGreen} 3}}={\color{Red} 4.3}.\sqrt{{\color{DarkGreen} 2.3}}={\color{Red} 12}\sqrt{{\color{DarkGreen} 6}}$

$\begin{align*}3.\;\;\;{\color{Red} 3\sqrt{2}}\left ( {\color{DarkGreen} 4\sqrt{5}}+{\color{DarkGreen} 2\sqrt{3}} \right )&=&\left ({\color{Red} 3\sqrt{2}}\times {\color{DarkGreen} 4\sqrt{5}} \right )+\left ({\color{Red} 3\sqrt{2}}\times {\color{DarkGreen} 2\sqrt{3}} \right )\\&=&12\sqrt{5}+6\sqrt{6}\end{align*}$

Merasionalkan Penyebut Bentuk Akar

ingat bahwa $(a+b)(a-b)=a^2-b^2$ maka berlaku pula pada bentuk akar sehingga :

$\begin{align*} (\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})&=&\left (\sqrt{a} \right )^2-\left (\sqrt{b} \right )^2\\&=&a-b\end{align*}$

A. Bentuk $\frac{a}{\sqrt{b}}$

Untuk merasionalkan penyebut bentuk akar 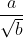$\frac{a}{\sqrt{b}}$ maka kita kalikan dengan penyebut bentuk akar tersebut ( kalikan dengan 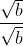$\frac{\sqrt{b}}{\sqrt{b}}$ yaaaaa…..)

Contoh soal :

$\begin{align*} \frac{3\sqrt{2}}{\sqrt{5}}&=&\frac{3\sqrt{2}}{\sqrt{5}}\times \frac{\sqrt{5}}{\sqrt{5}}\\&=&\frac{3\sqrt{10}}{\sqrt{25}}\\&=&\frac{3}{5}\sqrt{10}\end{align*}$

B. Bentuk $\frac{p}{\sqrt{a}+\sqrt{b}}$ atau $\frac{p}{\sqrt{a}-\sqrt{b}}$

Untuk merasionalkan penyebut bentuk akar seperti ini maka kita kalikan dengan sekawan penyebut bentuk akar tersebut.

Sekawan dari 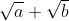$\sqrt a+\sqrt b$ adalah ${\color{Red} \sqrt a-\sqrt b}$

Sekawan dari 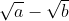$\sqrt a-\sqrt b$ adalah ${\color{Red} \sqrt a+\sqrt b}$

* ingat $\left({{\color{Red} \sqrt{a}+\sqrt{b}}} \right )\left ({{\color{Red} \sqrt{a}-\sqrt{b}}} \right )={\color{Red} a-b}$

Contoh Rasionalkan penyebut bentuk akar di bawah ini :

$\begin{align*}1.\:\:\:\frac{5}{\sqrt{3}+\sqrt{7}}&=&\frac{{\color{Red} 5}}{{\color{Red} \sqrt{3}+\sqrt{7}}}\times \frac{{\color{DarkGreen} \sqrt{3}-\sqrt{7}}}{{\color{DarkGreen} \sqrt{3}-\sqrt{7}}}\\&=& \frac{{\color{Red} 5}\left ( {\color{DarkGreen} \sqrt{3}-\sqrt{7}} \right )}{{\left (\color{Red} \sqrt{3}+\sqrt{7} \right )}\left ( {\color{DarkGreen} \sqrt{3}-\sqrt{7}} \right )}\\&=&\frac{{\color{Red} 5}{\color{DarkGreen} \sqrt{3}}-{\color{Red} 5}{\color{DarkGreen} \sqrt{7}}}{3-7}\\&=&\frac{5\sqrt{3}-5\sqrt{7}}{-4}\\&atau&\\&=&-\frac{5}{4}\left ( \sqrt{3}-\sqrt{7} \right )\end{align*}$

Nah, bagaimana dengan contoh lainnya? (ayuuuuk kita coba akar yang agak ribet dikit kali yeee…)

* ingat ${\color{Red} (\sqrt a+\sqrt b)(\sqrt a-\sqrt b)=(\sqrt a)^2-(\sqrt b)^2=a-b}$

$\begin{align*}2.\;\;\;\frac{2\sqrt{5}}{3\sqrt{2}-\sqrt3}&=&\frac{2\sqrt{5}}{3\sqrt{2}-\sqrt3}\times \frac{{\color{Red} 3\sqrt{2}+\sqrt{3}}}{{\color{Red} 3\sqrt{2}+\sqrt{3}}}\\&=&\frac{2\sqrt5\left ( {\color{Red} 3\sqrt{2}+\sqrt{3}} \right )}{\left ( 3\sqrt{2}-\sqrt{3}\right )\color{Red}\left ( 3\sqrt{2}+\sqrt{3} \right )}\\&=&\frac{2\sqrt5.{\color{Red} 3\sqrt2}+2\sqrt5.{\color{Red} \sqrt3}}{\left ( {\color{Red} 3\sqrt2} \right )^2-\left ( {\color{Red} \sqrt3} \right )^2}\\&=&\frac{6\sqrt{10}+2\sqrt{15}}{{\color{Red} 9.2}\;-\;{\color{Red} 3}}\\&=&\frac{6\sqrt{10}+2\sqrt{15}}{{\color{Red} 18}\;-\;{\color{Red} 3}}\\&=&\frac{6\sqrt{10}+2\sqrt{15}}{15}\\&atau&\\&=&\frac{2}{15}\left ( 3\sqrt{10}+\sqrt{15} \right ) \end{align*}$

soal penuh konsentrasi, tetapi sungguh menegangkan dan menyenangkan...

I love Math

Rabu, 28 November 2012

Perpangkatan dan akar

2 komentar: